Let O be the centre of circle M be mid point of AB.
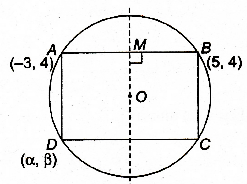
Then , OM \(\perp\) AB \(\Rightarrow\) M (1,4)
Since, slope of AB = 0
Equation of straight line MO is x = 1 and equation of diameter is \(4y = x + 7\).
\(\Rightarrow\) Centre is (1, 2).
Also, O is mid point of BD
\(\Rightarrow(\frac{\alpha+5}{2},\frac{\beta+4}{2})=(1,2)\)
\(\Rightarrow\alpha =-3,\beta =0\)
\(\therefore AD=\sqrt{(-3+3)^2+(4-0)^2}=4\)
and \(AB=\sqrt{64+0}=8\)
Thus, area of rectangle is \(8\times4=32\;sq\;unit\)