Question

Pythagoras theorem with formula and proof

Answer 1

Pythagoras theorem 

In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.

\(AC^2=AB^2+BC^2\)

 Proof 

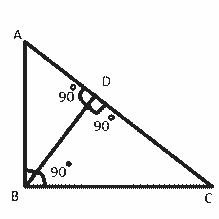
We know, △ADB ~ △ABC

Therefore, \(\tfrac{AD}{AB}=\tfrac{AB}{AC} \)(corresponding sides of similar triangles)

Or, AB² = AD × AC ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore, \(\tfrac{CD}{BC}=\tfrac{BC}{AC}\) (corresponding sides of similar triangles)

Or, BC²= CD × AC ……………………………………..(2)

Adding the equations (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.

Download img file for quick revision offline