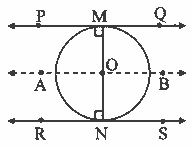
Let the lines PQ and RS be the two parallel tangents to circle at M and N respectively. Through centre O, draw line AB || line RS.
OM = ON = 4.5 [Given]
line AB || line RS [Construction]
line PQ || line RS [Given]
∴ line AB || line PQ || line RS
Now, ∠OMP = ∠ONR = 90° (i) [Tangent theorem]
For line PQ || line AB,
∠OMP = ∠AON = 90° (ii) [Corresponding angles and from (i)]
For line RS || line AB,
∠ONR = ∠AOM = 90° (iii) [Corresponding angles and from (i)]
∠AON + ∠AOM = 90° + 90° [From (ii) and (iii)]
∴ ∠AON + ∠AOM = 180°
∴ ∠AON and ∠AOM form a linear pair.
∴ ray OM and ray ON are opposite rays.
∴ Points M, O, N are collinear. (iv)
∴ MN = OM + ON [M – O – N, From (iv)]
∴ MN = 4.5 + 4.5
∴ MN = 9 cm
∴ Distance between two parallel tangents PQ and RS is 9 cm.