Question

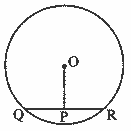
In the adjoining figure, seg QR is a chord of the circle with centre O. P is the midpoint of the chord QR. If QR = 24, OP = 10, find radius of the circle. To find solution of the problem, write the theorems that are useful. Using them, solve the problem. (Textbook pg. no. 48)

Answer 1

Theorems which are useful to find solution:
i. The segment joining the centre of a circle and the midpoint of a chord is perpendicular to the chord.
ii. In a right angled triangle, sum of the squares of the perpendicular sides is equal to square of its hypotenuse.
QP = \(\frac { 1 }{ 2 } \) (QR) [P is the midpoint of chord QR]

\(\frac { 1 }{ 2 } \) × 24 = 12 units
Also, seg OP ⊥ chord QR [The segment joining centre of a circle and midpoint of a chord is perpendicular to the chord]
In ∆OPQ, ∠OPQ = 90°
∴ OQ2 = OP2 + QP2 [Pythagoras theorem]
= 102 + 122
= 100 + 144
= 244
∴ OQ = \(\sqrt { 244 }\) = 2\(\sqrt { 61 }\) units.
∴ The radius of the circle is 2\(\sqrt { 61 }\) units.