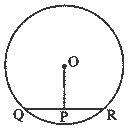
In the adjoining figure, seg QR is a chord of the circle with centre O. P is the midpoint of the chord QR. If QR = 24, OP = 10, find radius of the circle. To find solution of the problem, write the theorems that are useful. Using them, solve the problem. (Textbook pg. no. 48)