IVP Question paper solution DEC 2023

IVP Question paper solution DEC 2023 – AI&DS

Q.1 Solve any Four out of Five 5 marks each

A Justify : Describe the image in terms of the number of grey levels. Greyscale numbers are 2, 8, 64, and 256 are given. How does a change in the number of grey levels affects storage?. Explain with an example. IVP

The number of gray levels in a grayscale image directly impacts the amount of storage required to represent it. This relationship is determined by the number of bits allocated per pixel (bits per pixel or bpp).

Bits per Pixel (bpp): This value specifies how many bits are used to store the intensity information for a single pixel in the image.
Gray Levels: The number of gray levels an image can display is calculated as 2 raised to the power of bpp (2^bpp).

Impact on Storage:

More Gray Levels (Higher bpp):
- Provides finer detail in the image due to more shades of gray.
- Requires more storage space because each pixel needs more bits to represent a wider range of intensities.
Fewer Gray Levels (Lower bpp):
- Offers less detail due to a limited range of gray shades.
- Takes up less storage space as fewer bits are needed per pixel.

Example:

Suppose we have a grayscale image with dimensions of 1000×1000 pixels.

With 2 grey levels: Each pixel requires 1 bit (0 or 1). So, the total storage needed would be 1000 * 1000 * 1 bit = 1,000,000 bits.
With 8 grey levels: Each pixel requires 3 bits. So, the total storage needed would be 1000 * 1000 * 3 bits = 3,000,000 bits.
With 64 grey levels: Each pixel requires 6 bits. So, the total storage needed would be 1000 * 1000 * 6 bits = 6,000,000 bits.
With 256 grey levels: Each pixel requires 8 bits. So, the total storage needed would be 1000 * 1000 * 8 bits = 8,000,000 bits.

As you can see, as the number of grey levels increases, the storage requirement per pixel and, consequently, the overall storage needed for the image also increases.

B Justify : The best filter for removing salt and pepper noise from an image is median filter. Justify with an example.

Answer : https://www.doubtly.in/q/filter-removing-salt-pepper-noise-image-median-filter/

C Justify: Two fundamental characteristics of gray level values serve as the basis of segmentation algorithms for gray scale images.

Two fundamental characteristics of gray level values that serve as the basis of segmentation algorithms for grayscale images are:

Intensity Variation: Gray level values represent the intensity or brightness of each pixel in an image. The variation in intensity across different regions of the image forms the basis for segmentation. Segmentation algorithms exploit these intensity variations to partition the image into meaningful regions or objects. For example, in an image with distinct foreground and background regions, segmentation algorithms analyze the intensity differences between these regions to delineate boundaries and separate objects of interest.
Spatial Continuity: In addition to intensity variation, spatial continuity refers to the tendency of neighboring pixels with similar gray level values to belong to the same region or object. Segmentation algorithms leverage spatial continuity to group pixels into coherent regions based on their proximity and similarity in intensity. By considering both intensity and spatial relationships, segmentation algorithms can accurately identify boundaries and separate objects in the image. Techniques such as region growing, where adjacent pixels are iteratively added to a region based on similarity criteria, exploit spatial continuity to achieve segmentation.

D Justify: Although run length coding is lossless, it may not always result in data compression.

E Explain any five video formats.

Video formats dictate how video data is encoded, compressed, and stored. Here are explanations of five common video formats:

MPEG-4 (MP4):
- MPEG-4 is a widely used video format known for its versatility and efficiency in balancing video quality and file size.
- It supports various codecs such as H.264 and H.265, enabling high-quality video compression.
- MP4 files can store not only video but also audio, subtitles, and metadata.
- It is compatible with a wide range of devices and platforms, making it a popular choice for streaming, sharing, and storing videos.
AVI (Audio Video Interleave):
- AVI is one of the earliest video container formats developed by Microsoft.
- It supports multiple codecs and is known for its simplicity and widespread compatibility.
- AVI files can contain both audio and video data, making them suitable for storing movies, video clips, and multimedia presentations.
- However, AVI files tend to have larger file sizes compared to more modern formats like MP4, as they may not utilize advanced compression techniques efficiently.
MOV (QuickTime File Format):
- MOV is a multimedia container format developed by Apple for storing audio, video, and other media types.
- It is closely associated with QuickTime Player and is commonly used on macOS and iOS devices.
- MOV files can contain multiple tracks, allowing for the storage of multiple audio and video streams, as well as subtitles and metadata.
- MOV supports various codecs, including H.264, ProRes, and Animation, making it suitable for a wide range of applications, from professional video editing to online streaming.
WMV (Windows Media Video):
- WMV is a video format developed by Microsoft for use with its Windows Media Player.
- It offers efficient compression and high-quality video playback, making it suitable for streaming and downloading videos over the internet.
- WMV files are compatible with Windows-based devices and platforms, but may require additional codecs or plugins for playback on other operating systems.
- While WMV files can achieve smaller file sizes compared to some other formats, they may sacrifice some quality in favor of compression.
FLV (Flash Video):
- FLV is a container format developed by Adobe for streaming video content over the internet.
- It is commonly associated with Adobe Flash Player and was widely used for online video distribution on platforms like YouTube and Vimeo.
- FLV files use the VP6 video codec and the MP3 audio codec, offering a good balance between quality and file size for web-based video streaming.
- However, with the decline of Flash technology, FLV has become less prevalent, giving way to more modern formats like MP4 and WebM for online video delivery.

Q.2 10 Marks each

A What is DFT? Explain any four properties of DFT.

The Discrete Fourier Transform (DFT) is a mathematical technique used to analyze the frequency content of discrete-time signals. It transforms a sequence of N complex numbers (representing a discrete signal) into another sequence of complex numbers, which represents the signal in the frequency domain. The DFT is widely used in various fields, including signal processing, image processing, communications, and audio processing.

Here are four important properties of the Discrete Fourier Transform (DFT):

Linearity: The DFT is a linear operation. This means that if you have two signals x1[n] and x2[n] with corresponding DFTs X1[k] and X2[k], and you add or scale these signals, the resulting DFT of the combined or scaled signal (c1 * x1[n] + c2 * x2[n]) is equal to the sum or scaled sum of their individual DFTs (c1 * X1[k] + c2 * X2[k]). Mathematically, this property can be expressed as: [ \text{DFT}(c_1x_1[n] + c_2x_2[n]) = c_1\text{DFT}(x_1[n]) + c_2\text{DFT}(x_2[n]) ]
Periodicity: The DFT of a sequence x[n] with N samples yields N frequency components. These frequency components are periodic with a period of N samples. This means that if you shift the input sequence by an integer multiple of N samples, the resulting DFT remains unchanged. Mathematically, this property can be expressed as: [ X[k] = X[k \mod N] ]
Circular Convolution Property: The DFT of the circular convolution of two sequences is equal to the element-wise product of their DFTs. This property is particularly useful in signal processing applications, such as filtering and modulation. Mathematically, for sequences x[n] and y[n] with DFTs X[k] and Y[k], the circular convolution property can be expressed as: [ \text{DFT}(x[n] \circledast y[n]) = X[k] \cdot Y[k] ]
Symmetry Properties: The DFT exhibits symmetry properties for real-valued input signals. If the input signal x[n] is real, the DFT has conjugate symmetry. This means that if X[k] is the DFT of x[n], then X[k] = X[N-k]* for k = 1 to N-1, where * denotes the complex conjugate. Additionally, for even-length real sequences, the DFT exhibits symmetry about the center, while for odd-length real sequences, the DFT exhibits symmetry about the midpoint between two center points.

B What is meant by an image histogram. Perform Histogram Equalization on a given data. Draw histogram of original and equalized histogram.

Answer : https://www.doubtly.in/q/meant-image-histogram-perform-histogram-equalization-data/

Q3 : 10 Marks each

A Explain Log & Power law transformation with suitable diagrams.

Logarithmic transformations

Logarithmic transformation further contains two type of transformation. Log transformation and inverse log transformation.

Log transformation

The log transformations can be defined by this formula

s = c log(r + 1).

Where s and r are the pixel values of the output and the input image and c is a constant. The value 1 is added to each of the pixel value of the input image because if there is a pixel intensity of 0 in the image, then log (0) is equal to infinity. So 1 is added, to make the minimum value at least 1.

During log transformation, the dark pixels in an image are expanded as compare to the higher pixel values. The higher pixel values are kind of compressed in log transformation. This result in following image enhancement.

The value of c in the log transform adjust the kind of enhancement you are looking for.

Input Image

Log Tranform Image

The inverse log transform is opposite to log transform.

Power – Law transformations

There are further two transformation is power law transformations, that include nth power and nth root transformation. These transformations can be given by the expression:

s=cr^γ

This symbol γ is called gamma, due to which this transformation is also known as gamma transformation.

Variation in the value of γ varies the enhancement of the images. Different display devices / monitors have their own gamma correction, that’s why they display their image at different intensity.

This type of transformation is used for enhancing images for different type of display devices. The gamma of different display devices is different. For example Gamma of CRT lies in between of 1.8 to 2.5, that means the image displayed on CRT is dark.

Correcting gamma.

s=cr^γ

s=cr^(1/2.5)

The same image but with different gamma values has been shown here.

For example

Gamma = 10

Gamma = 8

Gamma = 6

src : https://www.tutorialspoint.com/dip/gray_level_transformations.htm

B Write derivation for Sobel Edge detection operator. What is the advantage of Sobel operator?

Answer : https://www.doubtly.in/q/write-derivation-sobel-edge-detection-operator-advantage-sobel-operator/

Q.4 10 Marks each

A ) What is Image Transform? What are the significance of Image Transform? Write basis images of Discrete Hadamard Transform.

Answer here : https://www.doubtly.in/q/image-transform-significance-image-transform/

B ) Explain Vector Quantization (VQ) with example

Answer : https://www.doubtly.in/q/explain-vector-quantization-vq/

Q.5 10 Marks each

A Explain Composite and Component Video in detail (repeated)

Composite Video and Component Video are two different methods of transmitting video signals, each with its own characteristics and applications:

Composite Video:

Definition: Composite video combines all video information into a single signal.
Signal Structure: In composite video, luminance (brightness) and chrominance (color) information are combined into one signal. This means that the entire picture is transmitted as one signal through a single cable.
Connection: Typically, composite video uses a single RCA connector (yellow) for transmission.
Quality: Composite video is capable of transmitting standard definition video, but it suffers from signal degradation due to the mixing of luminance and chrominance information. This can result in issues such as color bleeding and reduced image sharpness.
Common Uses: Composite video was widely used in older consumer electronics devices such as VCRs, early DVD players, and older game consoles.

Component Video:

Definition: Component video separates the video signal into multiple components.
Signal Structure: Component video splits the video signal into three separate channels: luminance (Y), and two chrominance channels (Cb and Cr). This separation allows for better image quality and color accuracy compared to composite video.
Connection: Component video typically uses three RCA connectors (red, green, blue) or a set of three cables bundled together.
Quality: Component video offers higher quality than composite video, capable of transmitting both standard definition and high definition video signals. The separation of luminance and chrominance components reduces signal interference and improves image clarity.
Common Uses: Component video was commonly used in older high-definition displays, analog television sets, and certain video equipment. It has been largely replaced by digital interfaces like HDMI in newer devices.

Comparison Table:

Aspect	Composite Video	Component Video
Signal Structure	Combines luminance and chrominance	Separates luminance and chrominance
Number of Cables	Single cable (typically RCA)	Three cables (RCA or bundled)
Image Quality	Lower quality, prone to interference	Higher quality, better color accuracy
Resolution Support	Standard definition	Standard and high definition
Connection	Simple, single cable connection	Requires multiple cables
Common Uses	Older consumer electronics	Older high-definition displays

B ) Explain Arithmetic Coding in detail

Arithmetic coding is a type of entropy encoding used in lossless data compression. Typically, a string of characters, for example, the word “hey,” is represented using a fixed number of bits per character.

In the simplest case, the probability of each symbol occurring is equal. Consider a set of three symbols: A, B, and C, each equally likely to occur. Simple block encoding would require 2 bits for each symbol, which is inefficient because one of the bit variations is rarely used. For example, A = 00, B = 01, and C = 10, but 11 is unused. A more efficient approach is to represent a sequence of these three symbols as a rational number in base 3, where each digit represents a symbol. For instance, the sequence “ABBCAB” could become 0.011201 in arithmetic coding as a value in the range [0, 1). The next step is to encode this ternary number using a fixed-point binary number with sufficient precision to recover it, such as 0.0010110010₂—this is just 10 bits. This is feasible for long sequences because there are efficient, established algorithms for converting between bases of arbitrarily precise numbers.

In general, arithmetic coders can produce nearly optimal output for any given sequence of symbols and probabilities (the ideal value is –log₂P bits for each symbol with probability P). Compression algorithms that use arithmetic coding work by determining a structure of the data—essentially a prediction of what patterns will be found in the symbols of the message. The more accurate this prediction is, the closer to optimal the output will be.

For each step of the encoding process, except the very last, the procedure is the same; the encoder mainly has three pieces of information to consider:

The next symbol that needs to be encoded.
The current range (at the very start of the encoding process, the range is set to [0, 1], but this will change).
The probabilities the model assigns to each of the different symbols that are possible at this stage (as mentioned earlier, higher-order or adaptive models mean that these probabilities are not necessarily the same in each step).

The encoder divides the current range into sub-ranges, each representing a fraction of the current range relative to the probability of that symbol in the current context. The sub-range corresponding to the actual symbol to be encoded next becomes the range used in the next step. When all symbols have been encoded, the resulting range unambiguously identifies the sequence of symbols that produced it. Anyone with the same final range and model used can reconstruct the symbol sequence that must have entered the encoder to result in that final range. It is not necessary to transmit the final range; it is only necessary to transmit one fraction that lies within that range. Specifically, it is only necessary to transmit enough digits (in any base) of the fraction so all fractions that start with those digits fall into the final range; this will ensure that the resulting code is a prefix code.

src : https://www.geeksforgeeks.org/arithmetic-encoding-and-decoding-using-matlab/

Q.6 10 Marks each (Short Note)

A ) Compare Discrete Fourier Transform & Fast Fourier Transform. Calculate DFT for following 4×4 image

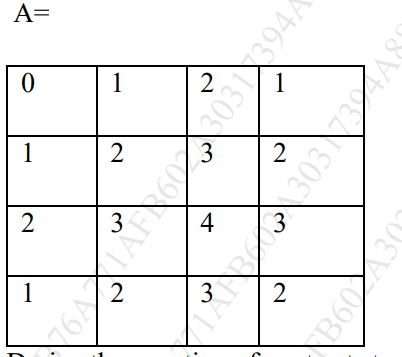
Answer :

Aspect	Discrete Fourier Transform (DFT)	Fast Fourier Transform (FFT)
Computational Complexity	( O(N^2) )	( O(N \log N) )
Algorithm Speed	Slower for large data sets	Faster for large data sets
Time Complexity	( O(N^2) )	( O(N \log N) )
Space Complexity	( O(N) )	( O(N) )
Usage	Basic form of Fourier analysis. Used for small datasets.	Widely used for larger datasets in signal processing applications.
Memory Requirement	High memory usage due to (N^2) operations.	Lower memory usage due to divide-and-conquer approach.
Data Dependency	High data dependency.	Low data dependency.
Implementation Ease	Conceptually simpler to implement.	More complex due to algorithm intricacies.
Optimizations	Fewer optimization opportunities.	Numerous optimizations available, including radix-2 and radix-4.
Speed vs. Accuracy	Slower but more accurate for small datasets.	Faster and still accurate for larger datasets.

Explanation of DFT:

DFT is a mathematical technique used in signal processing and spectral analysis to analyze the frequency content of a discrete signal. It transforms a signal from its time-domain representation to its frequency-domain representation. The DFT essentially decomposes a sequence of values into a sum of sinusoids of different frequencies. However, the direct computation of DFT involves (N^2) complex multiplications and additions, making it computationally expensive, especially for large datasets.

Explanation of FFT:

FFT is an algorithm used to compute the DFT efficiently. It exploits the symmetry properties of the Fourier transform to reduce the number of operations required from (O(N^2)) to (O(N \log N)). This reduction in computational complexity makes FFT significantly faster than the naive DFT algorithm, especially for large datasets. FFT is widely used in various fields such as signal processing, image processing, and data compression due to its computational efficiency.

Numerical : https://www.doubtly.in/q/calculate-dft-4×4-image/

B ) Derive the equation of contrast stretching transformation function as given below. Apply the contrast stretching transformation function on the input image F and obtain output image R

Answer : https://www.doubtly.in/q/derive-equation-contrast-stretching-transformation-function/

Table of Contents